因数分解を図形の面積から導き証明も図形をすべてつかい表している。 一意性の観点からは因数分解を導いていない。 素数 ゜ 次の乗沵公式を用いる式の展開と因数分解。 教科書 新編 新しい数学3 東京書籍, 単元 多項式の計算,因数分解,式の計算の利用, 「中学校3年生の展開・因数分解を利用した応用問題を解いたノートです。 授業ノートなので見にくいところはあしからず SPというのは先生が作ってくださったオリジナルのスペシャル問題という意味です3 因数分解を利用して,次の式の値を求めなさい。(途中の計算も書きなさい。) x =2のとき,x 2-4x +4の値 解答 ア イ ウ 第3学年 1 式の展開と因数分解 B B BLB1 X Î 0 ÉwBèB B

三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ
式の展開と因数分解 証明
式の展開と因数分解 証明-式の計算② 公式展開(標準) 公式展開(応用) 公式展開(発展) (展開)計算への利用;練習プリントをダウンロード https//ecommonsbiz/wpcontent/uploads//07/DB033pdf 動画リンク 文字式による説明(前半:整数、偶数



因数分解のやり方 公式と解き方のコツ教えます 高校レベルまで対応 Studyplus スタディプラス
行列式 (4)基本性質による因数分解 == 行列式の基本性質を用いた因数分解 == このページでは,行列式の基本性質を使って,文字式の値を求める問題を扱う. 以下においては,これらの基本性質のうちで,主に次の2つを使って,文字式の変形を行う練習プリントをダウンロード https//ecommonsbiz/wpcontent/uploads//07/DB035pdf 動画リンク 文字式を使った証明(展開・因数分解編3年「式の展開と因数分解」 氏名 このことを、次のように証明した。 にあてはまる式を書きなさい。 (証明) 連続する2つの奇数は、整数nを使って、2n+1、 と表される。それらの2乗の差は、
証明は展開すれば分かるので省略.ここでは次の点に注意したい. 例えば (x5) (x3)=x2 8 x 15 などとする. また, (x5a) (x3a)=x2 8a x 15a 2 などとする. さらに, (xa3) (xa2)=x2 (2a5) x (a 2 5a6) などとする. この公式は「総当たりで全部掛ける」というの①2つの整数の小さい方を としたとき、 大きい方の整数を式 で表しなさい。 ②2乗の差と2数の和を式で表し、等しいことを証明しなさい。 連続する3つの整数では、中央の数の2乗から1をひくと、両端の数の積に 等しくなることを証明しなさい。 2 n n 2 n nルート2が無理数であることの4通りの証明 レベル ★ 入試対策 式の計算 更新日時 2 \sqrt {2} 2 は無理数である。 より一般に,平方数でない正の整数
もくじ 1 分配法則で多項式同士の掛け算を証明する 11 4つの乗法公式を使った式の展開; 中3 学習単元一覧 式の展開 因数分解 平方根 2次方程式 2乗に比例する関数 図形の相似 三平方の定理 円の性質 標本調査 式の展開式の展開の基礎乗法公式1乗法公式2因数分解の発展公式 因数分解公式(3つの立方和) 3変数の相加相乗平均の証明などに用いる有名公式です。 因数分解公式(n乗の差,和) 等比数列の和にまつわる因数分解公式です。整数問題に応用されます。 因数分解公式(ソフィージェルマンの恒等式)



中学数学 式による説明 図形 中学数学の無料オンライン学習サイトchu Su




中3 式の計算の利用 円 正方形の図形の証明をイチから 数スタ
2 因数分解:かっこの式を作る 21 因数分解は複数の選択肢がある;除法を行なうと、 が得られるが、(x4)(x3)に因数分解できる。答えは、 () () となる。 高次方程式 因数分解や因数定理を利用して高次方程式を解いてみよう。 問題例;因数分解 16 (xa)(xb)の展開 アニメーション 1章 式の展開と 因数分解 17 平方の公式 アニメーション 1章 式の展開と 因数分解 18 和と差の積の公式 アニメーション 1章 式の展開と 因数分解 数学ライブラリー (公式から公式を導く) スライド
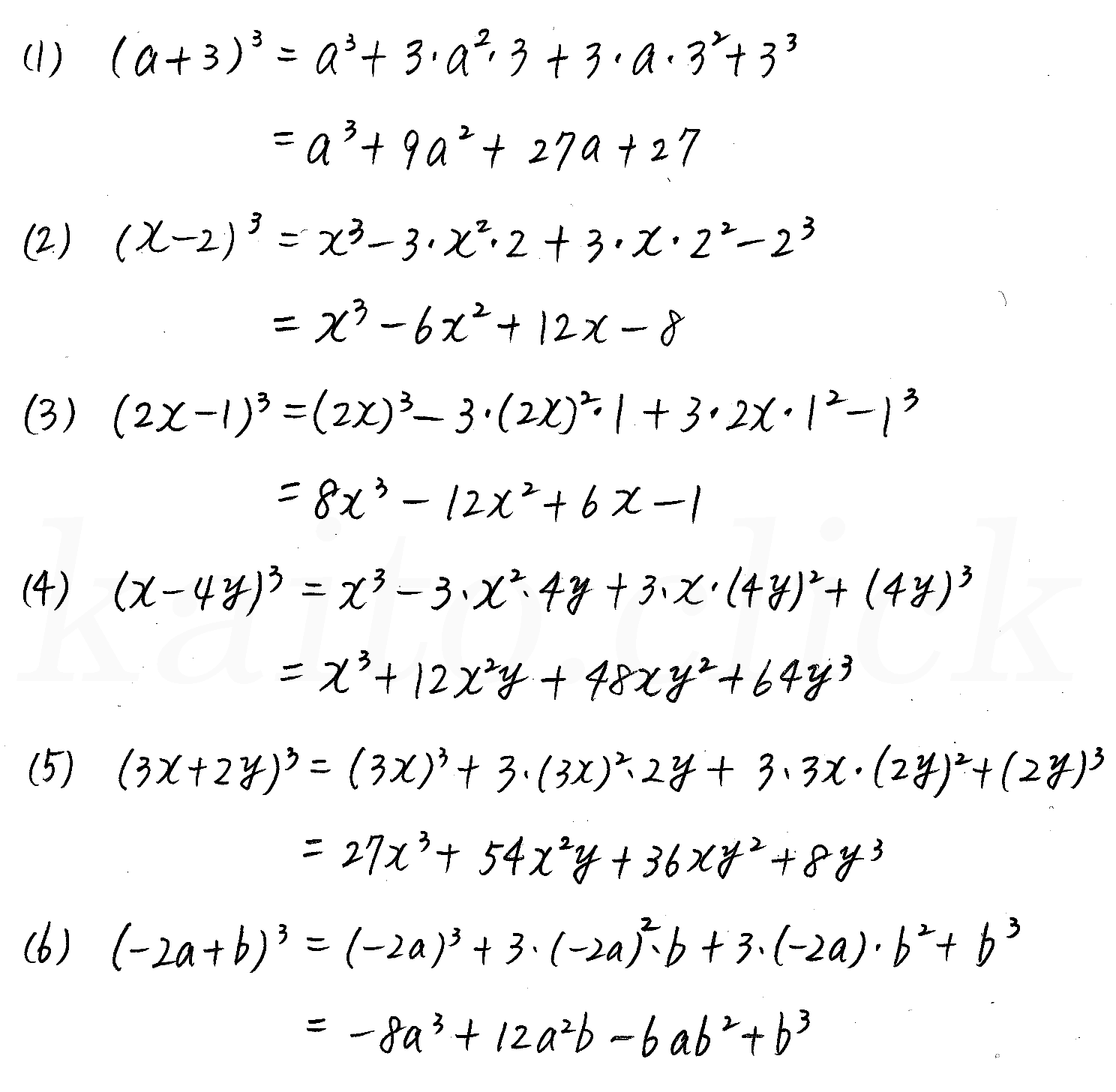



改訂版 3trial数学 P6 1 3次式の展開と因数分解




中3 展開と因数分解22 式の計算の利用4 中学数学の勉強に
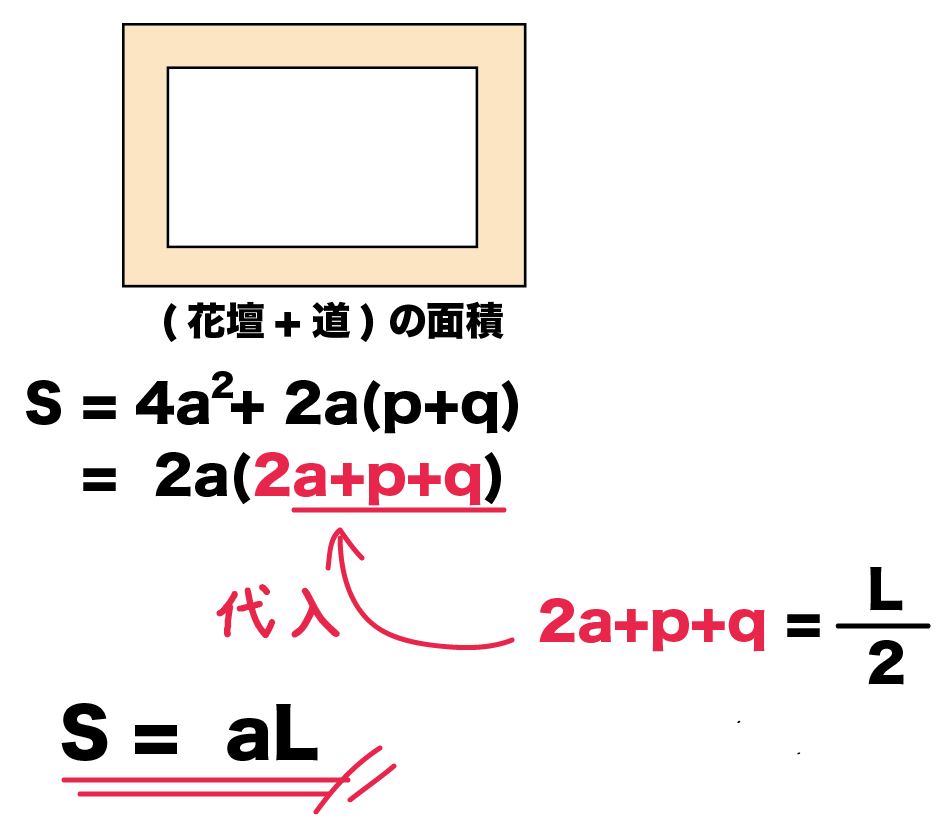
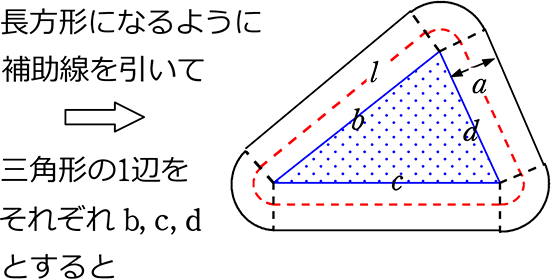
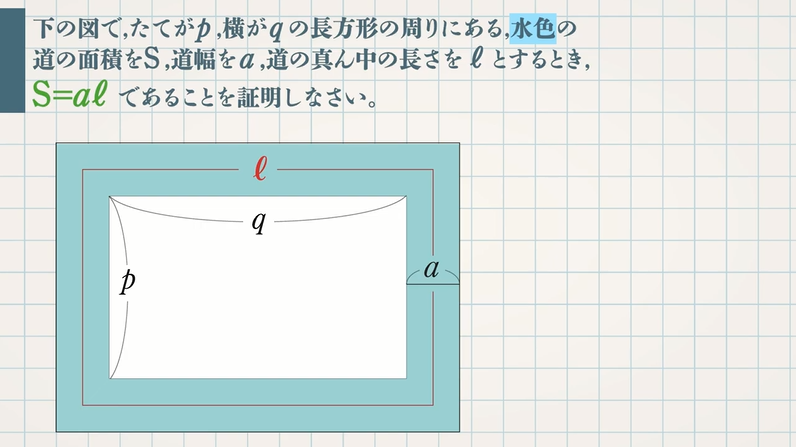
${\rm S}=aℓ$ の証明は次の $3$ つのSTEPで解くので、しっかり流れを確認しましょう。 STEP①:大きい方の図形から小さい方の図形を引いて、 $\textcolor{blue}{{\rm S}}$ (道の面積)を $\textcolor{blue}{a,p,q}$ を用いた式で表す STEP②: $\textcolor{blue}{ℓ}$ (道の真ん中の長さ)を $\textcolor{blue}{a,p,q}$ を用いた3年「式の展開と因数分解」 氏名 このことを、次のように証明した。 にあてはまる式を書きなさい。 (証明) 連続する2つの奇数は、整数nを使って、2n+1、 と表される。それらの2乗の差は、第1章 式の展開と因数分解 <前:L7 因数分解(3)‐乗法公式の利用2 の問題 L8 式の展開・因数分解の利用 の解答:次> 練習問題1 連続する2つの偶数の積に1をたすと、その2つの偶数の間の奇数の2乗になる。 このことを証明しなさい。 練習問題2




展開 因数分解の利用 式の証明 清水塾




高校数学 展開公式の利用 受験の月
応用分野: 放物線の定積分, 式の展開と因数分解, 因数分解の手順, 因数分解 (x^2x1)(x^2x1), 因数分解, 問題リスト ←このページに関連している問題です式と証明 1 (1) 次の式を展開せよ。 ① (x+1)(x2-x+1) ② (2a-b)(4a2+2ab+b2) ③ (x+3)3 ④ (3a-2b)3 (2) 次の式を因数分解せよ。 ① x3+27 ②になることを証明しなさい。 5510 15 25 30 35 40 45 6612 18 24 30 36 42 48 54 7714 21 28 35 42 49 56 63 16 24 32 40 48 56 64 72 9918 27 36 45 54 63 72 81 数学31章式の展開と因数分解



Http Www Kita9 Ed Jp Eductr Handbook Challengesheet Juniorhighschool Suugaku 3 1 Pdf



1
展開や因数分解を使って,条件に合うように式を変形し,図形の性質を説明することができる。 (2)本時の評価規準 ・文字を用いて表現したり,その意味を読み取り,条件に合うように式を変形し,図形の性質を 説明しようとしている。また, ~ の式を因数分解せよ。 三次の乗法公式,因数分解の公式及び二項 \ \ 定理を理解し,それらを用いて式の展開や \ \ 因数分解をすること。また,整式の除法や 例 d e を展開せよ。 分数式の四則計算について理解し,簡単な今回は文字式を使った証明(展開・因数分解編)です。 まずは復習です。文字式を利用すると数の関係や性質などいろいろな事柄の説明ができました。 連続する奇数を文字で表す→$2n1,2n3$ など 式の計算を利用して、さまざまな事柄を説明してみましょう。



式の計算の利用 図形の証明問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




中3数学 展開 因数分解 図形の証明 円 Youtube
因数分解の公式を乗 法の公式と関連付け て理解している。 数量及び数量の関係 を帰納や類推によっ て捉え、それを文字 式を使って一般的に 証明することができ ることを理解して いる。 式の展開や因数分解 は、文字式を使った 証明にも活用できる展開公式を丸ごと覚えるのではなく,導けるようにしましょう。 19 19 19 も同様に式の対称性と多項定理から一瞬で導けます。 このように対称式の展開は「対称性,多項定理,係数の和」に注目 して瞬時に行えるようになっておくのが理想です。と因数分解することできます。 次の式も同様に因数分解ができます。 $$4x^212xy9y^2\\ \\=(2x)^22\times 2x\times 3y(3y)^2\\ \\=(2x3y)^2$$ 因数分解をする式を見たとき、両サイドが二乗の形で表される場合には、この公式を使うのかな?と考えてみるといいですね。




文字式を使った証明 展開 因数分解編 教遊者




展開 因数分解の利用 図形への利用 無料で使える中学学習プリント
展開・因数分解の利用 式の証明② 問題はこちらです。 連続する3つの整数では、最大の整数と最小の整数の 積に1をたした数は中央の整数の2乗になる。 このことを中央の整数をnとして証明しなさい。 解答と解説は下にあります。 ☟ スポンサー動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru展開や因数分解の考え方を上手く利用すると、数字の計算がとても楽になる場合があるんだ。 POINT 64 2 -36 2 で見てみよう。 (2乗)-(2乗) 、 おなじみのラッキーパターン だね。 因数分解の公式を使って式を変形させると 64 2 -36 2 = (64+36)×




高校数学 4step 全問解説 数学 第1章 式と証明 3次式の展開と因数分解 二項定理 問題1 カリスマ塾長 タイガーblog




式の展開と因数分解の図形の証明です Clear




3次式の因数分解 公式とやり方について問題を使って解説 数スタ



中学数学 式の展開 因数分解
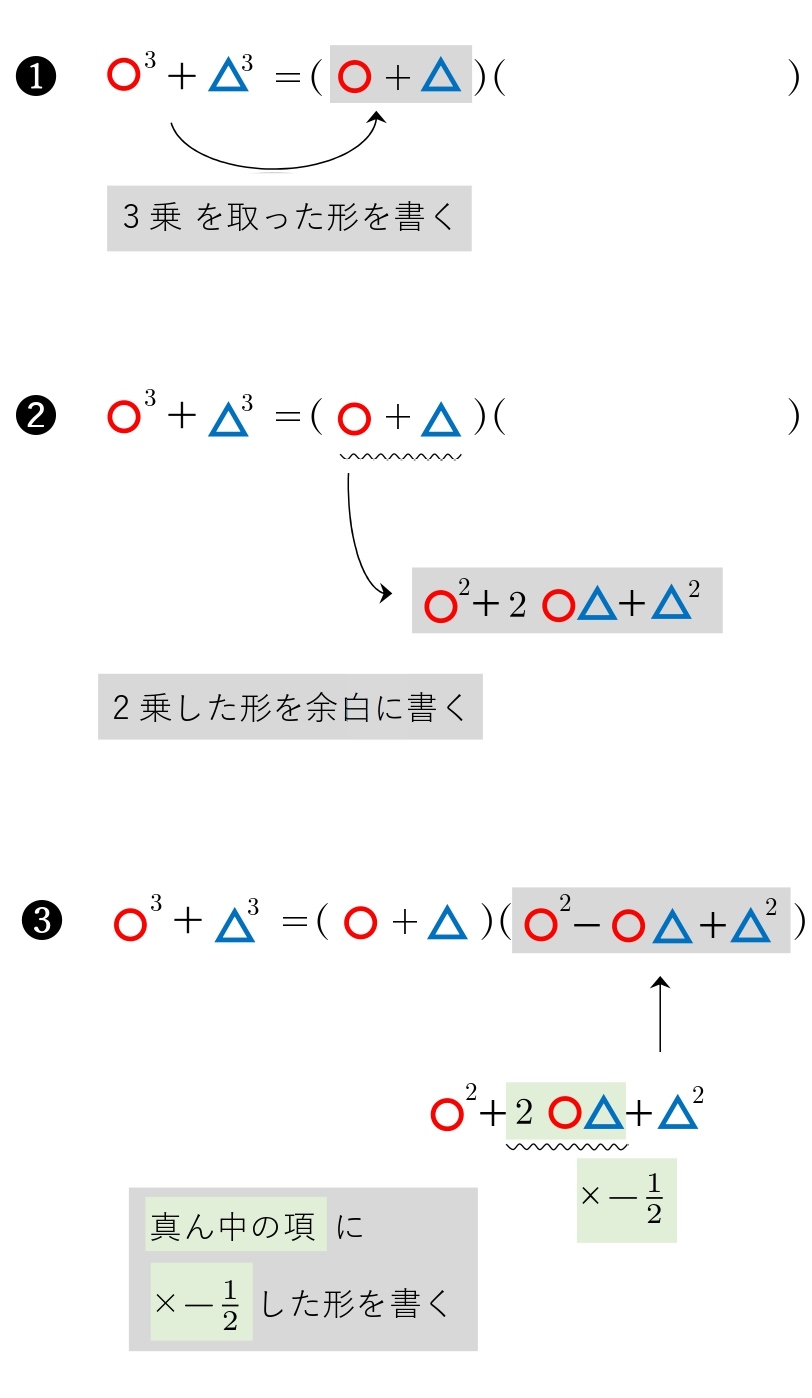



高校数学 3次式の展開 因数分解 公式 覚え方 計算方法 学校よりわかりやすいサイト



因数分解のやり方 公式と解き方のコツ教えます 高校レベルまで対応 Studyplus スタディプラス




3次式の因数分解 公式とやり方について問題を使って解説 数スタ




中学数学 式の展開 因数分解




3乗の因数分解 展開 公式 理系ラボ




中3 数学 式の展開と因数分解を利用した 図形の証明問題解説動画 S Al ページ 2




式と証明 3次式の展開について 日々是鍛錬 ひびこれたんれん
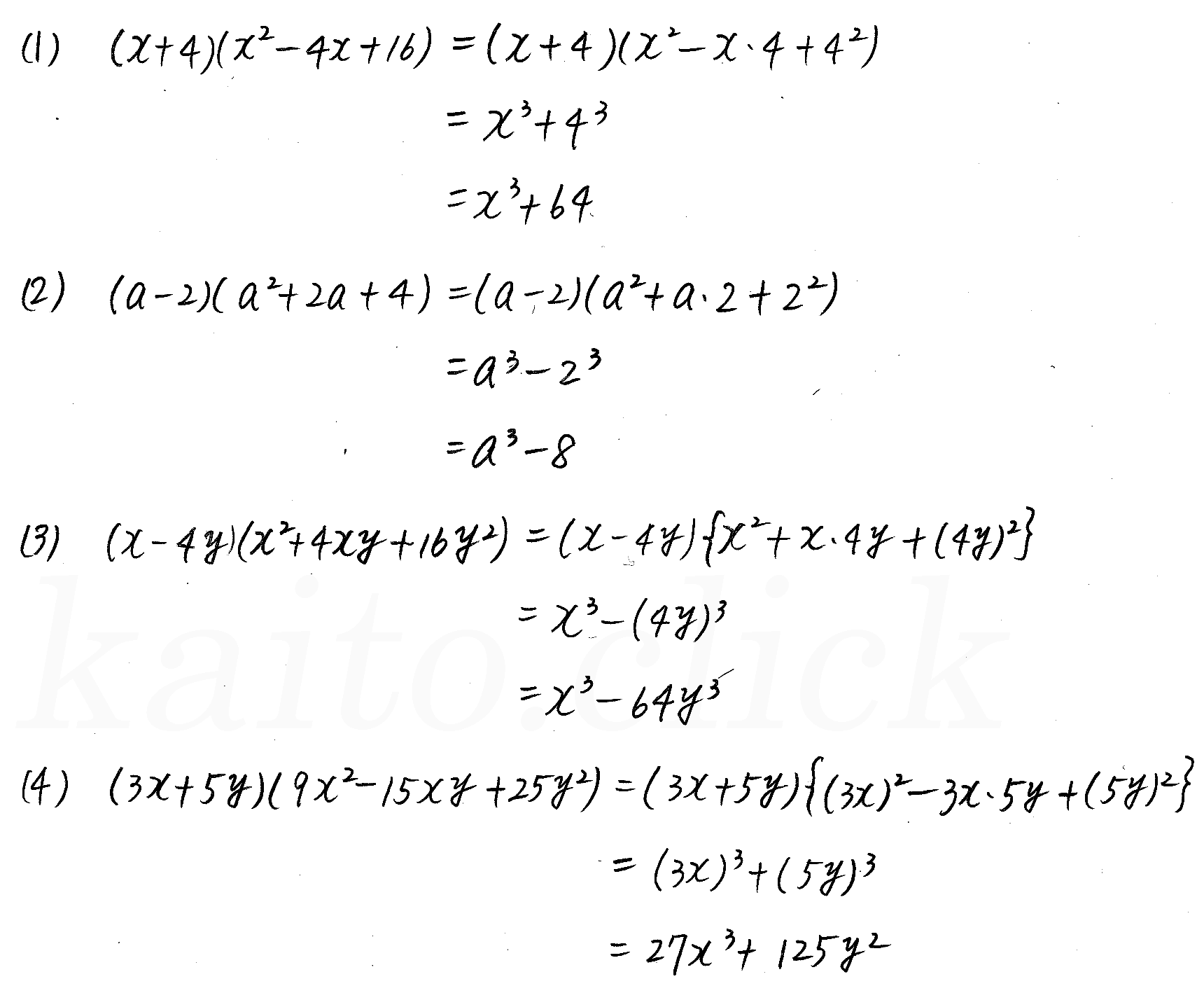



改訂版 3trial数学 P6 1 3次式の展開と因数分解



中学校3年生の数学の授業




乗法公式による式の展開と因数分解 中学数学の多項式計算 リョースケ大学




数学 B 3次式の展開 広島国際学院大 山形大 大学入試数学の考え方と解法
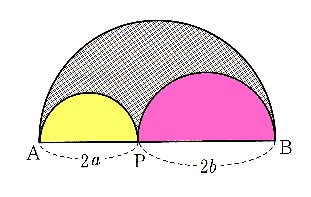



中学3年数学 式の展開と因数分解 式の計算の利用 練習問題4 解答 あんのん塾




高校数学 因数分解公式と3次式の因数分解 A B C 3abc 受験の月




式の計算の利用と練習問題 基 数学の解説と練習問題



1




天才数学者が考案した二次方程式 因数分解の新しい解き方 これは簡単で面白い 数学の面白いこと 役に立つことをまとめたサイト




展開 8 3文字3次の対称式 怜悧玲瓏 高校数学を天空から俯瞰する



Python




展開 因数分解の利用 証明 無料で使える中学学習プリント




展開と因数分解の利用 の問題のわからないを5分で解決 映像授業のtry It トライイット




1 B 1 21 22 Descubre Como Resolverlo En Qanda




乗法公式による式の展開と因数分解 中学数学の多項式計算 リョースケ大学



1




高校数学 3次式の展開 因数分解 公式 覚え方 計算方法 学校よりわかりやすいサイト




数学 中3 13 式の計算の利用 数字の証明編 Youtube



数学ii Bチェック リピート 第1章 1式と証明 1 3次式の展開 因数分解 Pukiwiki
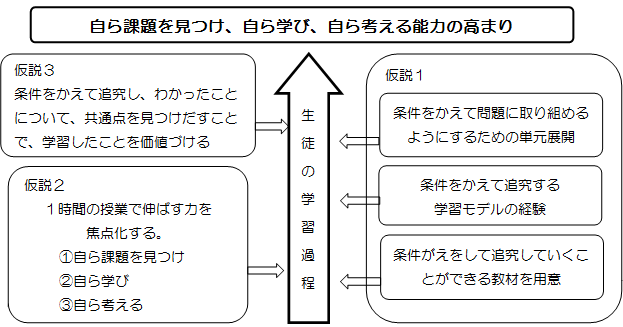



授業実践記録 数学 自ら課題を見つけ 自ら学び 自ら考える能力を高めるためには どのように教材を組織し指導したらよいか 啓林館




中3 展開と因数分解22 式の計算の利用4 中学数学の勉強に




数学 3次式の展開と因数分解 二項定理 式と証明 井出進学塾のマンツーマン授業の実況中継 井出進学塾 富士宮教材開発 公式ブログ Note




無料 中3数学 基本問題 問題プリント 304 式の計算4 素因数分解




中3 展開 因数分解 S Aℓの証明 式の計算の利用 図形編 Youtube




数学 中3 14 式の計算の利用 図の証明編 Youtube




3乗の因数分解 展開 公式 理系ラボ




中3数学 道路の面積を求める問題 例題編 映像授業のtry It トライイット




展開と因数分解の利用2 チーム エン



Www Kyo Kai Co Jp Img Material Chuu 1691 Sc S3 Mokuji Pdf




式と計算




1章 式の展開と因数分解 愛知県公立高校入試 数学 単元別過去問 問題プリントと解答 解説




中学数学 式の展開 因数分解




展開因数分解の式の値の応用 対称式と交代式 中3数学 高校受験ラボ




三乗 3乗の展開 因数分解の公式 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開



1



Http Tyu Oita Ed Jp Hita Mikuma E5 8d 98 E5 85 E8 A8 E7 94 Ef E7 Ac Ac Ef 93 E5 Ad A6 E5 B9 B4 80 80 Ef 91 E7 Ab A0 Ef 9a E5 8f 81 Ae E8 A8 E7 Ae 97 81 Ae E5 E7 94 A8 Ef Pdf




中学3年数学 式の展開と因数分解 式の計算の利用 練習問題3 あんのん塾




文字式を使った証明 展開 因数分解編 教遊者




文字式を使った証明 展開 因数分解編 教遊者




中学3年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ




高校数学 因数分解公式と3次式の因数分解 受験の月
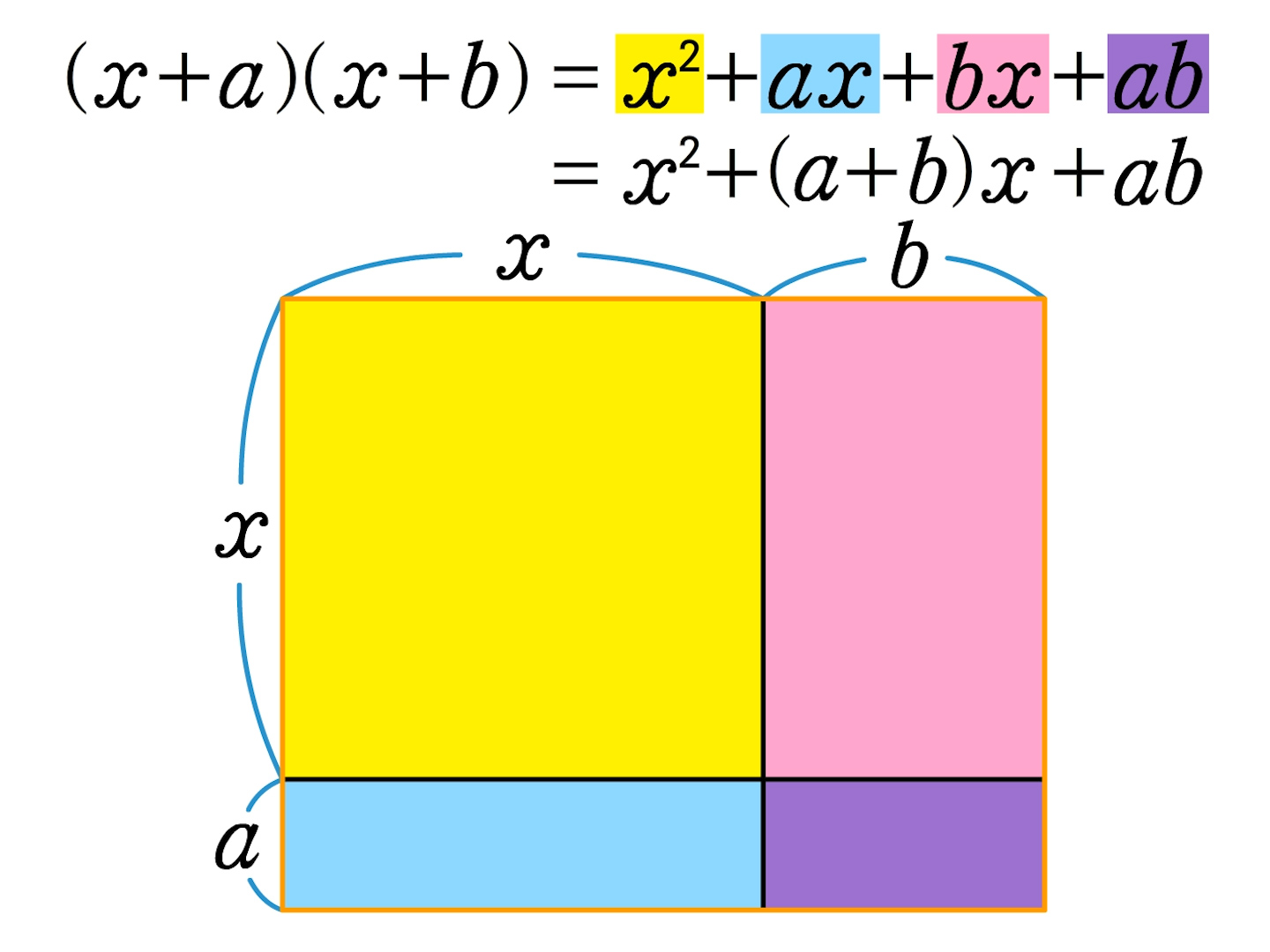



3年 図形で考えよう X A X B 数学イメージ動画集 大日本図書



式の計算の利用 展開と因数分解 中学3年 数学クラブ




3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す
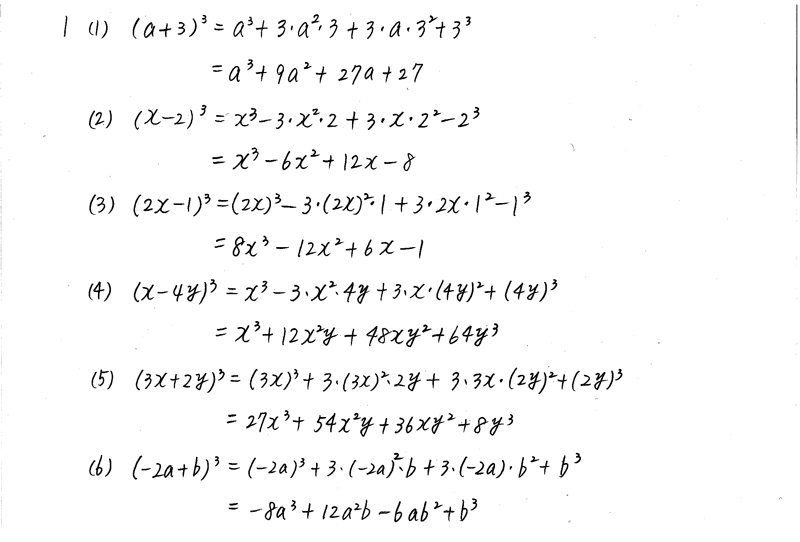



新課程 3trial数学 P6 1 3次式の展開と因数分解




中3 中3 数学 式の利用 中学生 数学のノート Clear



因数分解でやる 図形の証明がわかりません 正方形や長方形はできたのですが 長方 Yahoo 知恵袋




1講 3次式の展開と因数分解 1節 式と計算 問題集 1章 式と証明




無料 中3数学 基本解説 解答プリント 307 式の計算7 式の計算の利用




中学3年生です 式の展開と因数分解の範囲をしています Clear
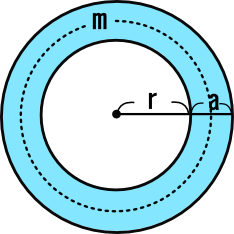



中学3年数学練習問題 式の利用 証明 式の展開 因数分解の応用




展開 因数分解の利用 証明 無料で使える中学学習プリント




中学数学 多項式 の教え方 式の計算の利用



三乗 3乗の展開 因数分解の公式 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開




S Alの証明 清水塾




展開 因数分解を利用する問題 鶴城数人 Note



2




式と証明 複雑な式の因数分解 数学 定期テスト対策サイト



中学三年生の式の展開と因数分解の利用の図形の性質の証明の仕方 Yahoo 知恵袋




中学3年生 数学 因数分解 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




式の計算の利用と練習問題 基 数学の解説と練習問題




中学数学 式の展開 因数分解
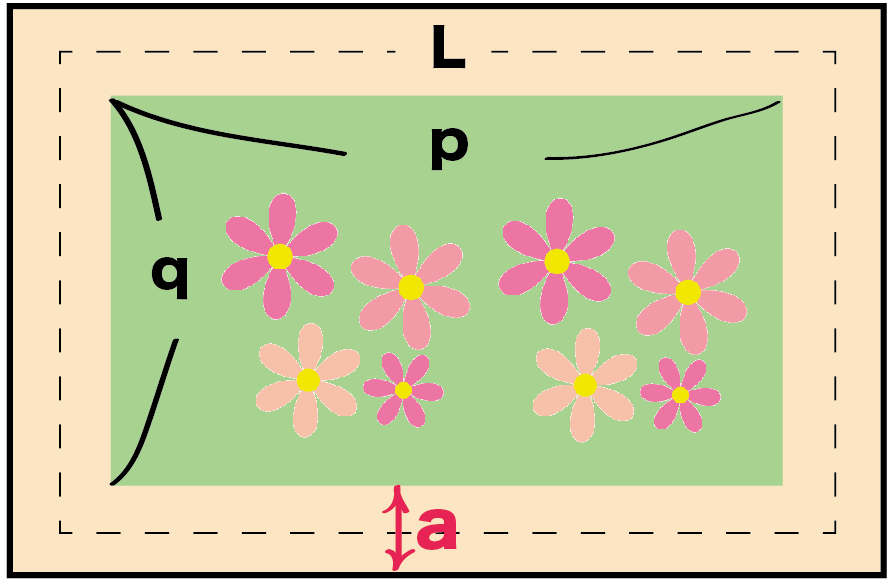



式の計算の利用 図形の証明問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




式の計算の利用と練習問題 基 数学の解説と練習問題



S Aℓの証明 式の計算の利用 図形編 教遊者
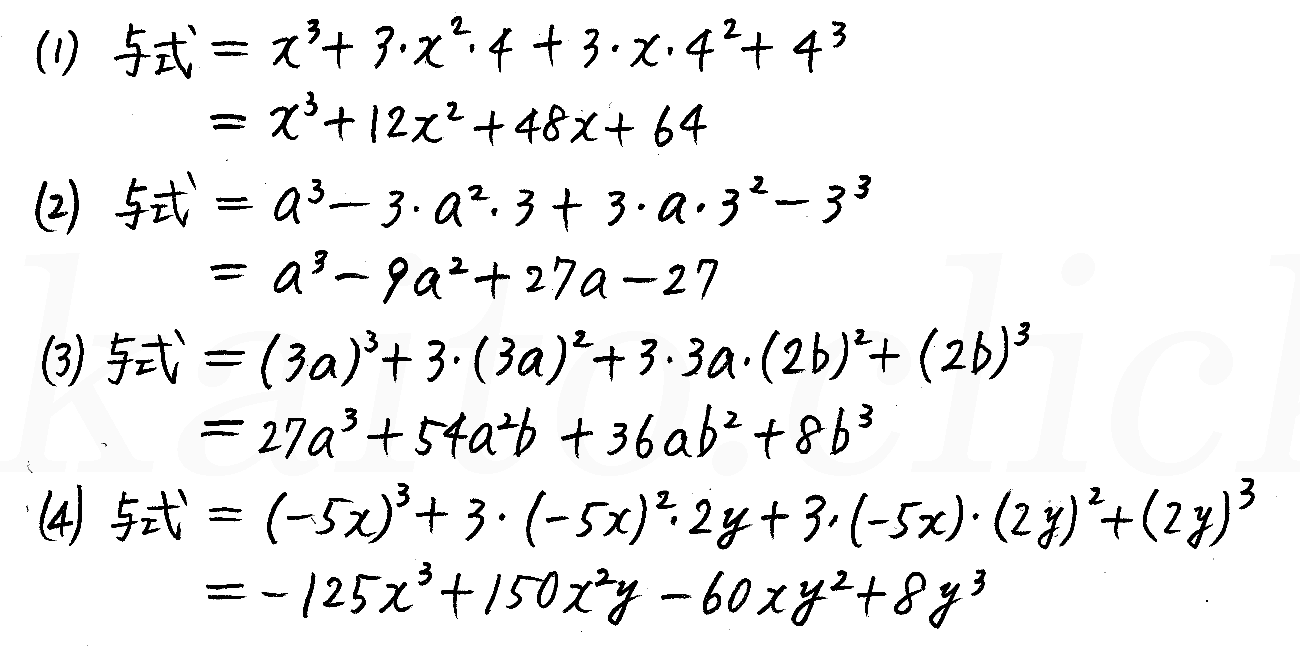



改訂版 4プロセス数学 P6 1 3次式の展開と因数分解




中学3年数学練習問題 式の利用 証明 式の展開 因数分解の応用



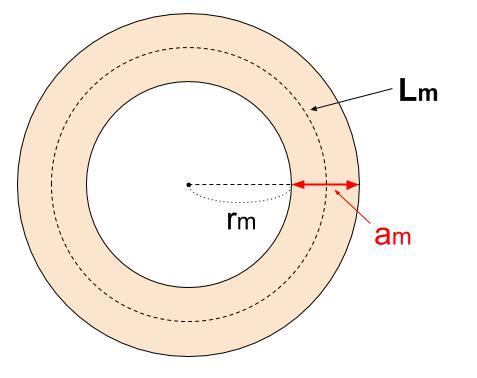
式の展開と因数分解を利用した証明 半径rの円形の花壇のまわりに 幅aの道が付 Yahoo 知恵袋




1講 3次式の展開と因数分解 1節 式と計算 問題集 1章 式と証明




展開 因数分解の利用 図形 清水塾




3次式の因数分解の公式を徹底解説



U9j580gf8iba369ji2w Xyz P 608




高校数学 数 11 因数分解 3次式の公式編 Youtube




三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ




世界一わかりやすい数学問題集中3 1章 式の展開と因数分解




展開 因数分解の利用 図形への利用 無料で使える中学学習プリント




Bar6 1 15 Lihat Cara Penyelesaian Di Qanda
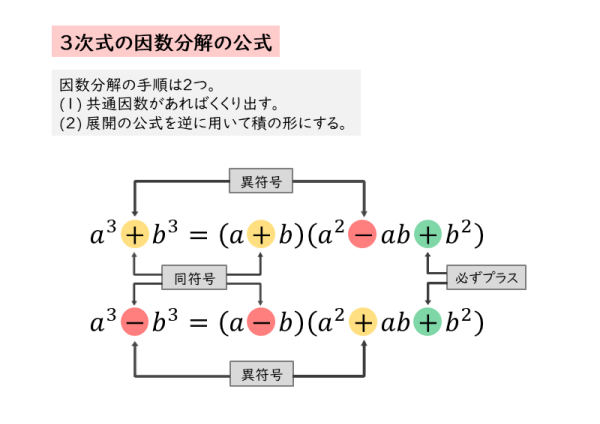



式と証明 3次式の因数分解について 日々是鍛錬 ひびこれたんれん




中3 中3数学 式の展開と因数分解 まとめ 中学生 数学のノート Clear
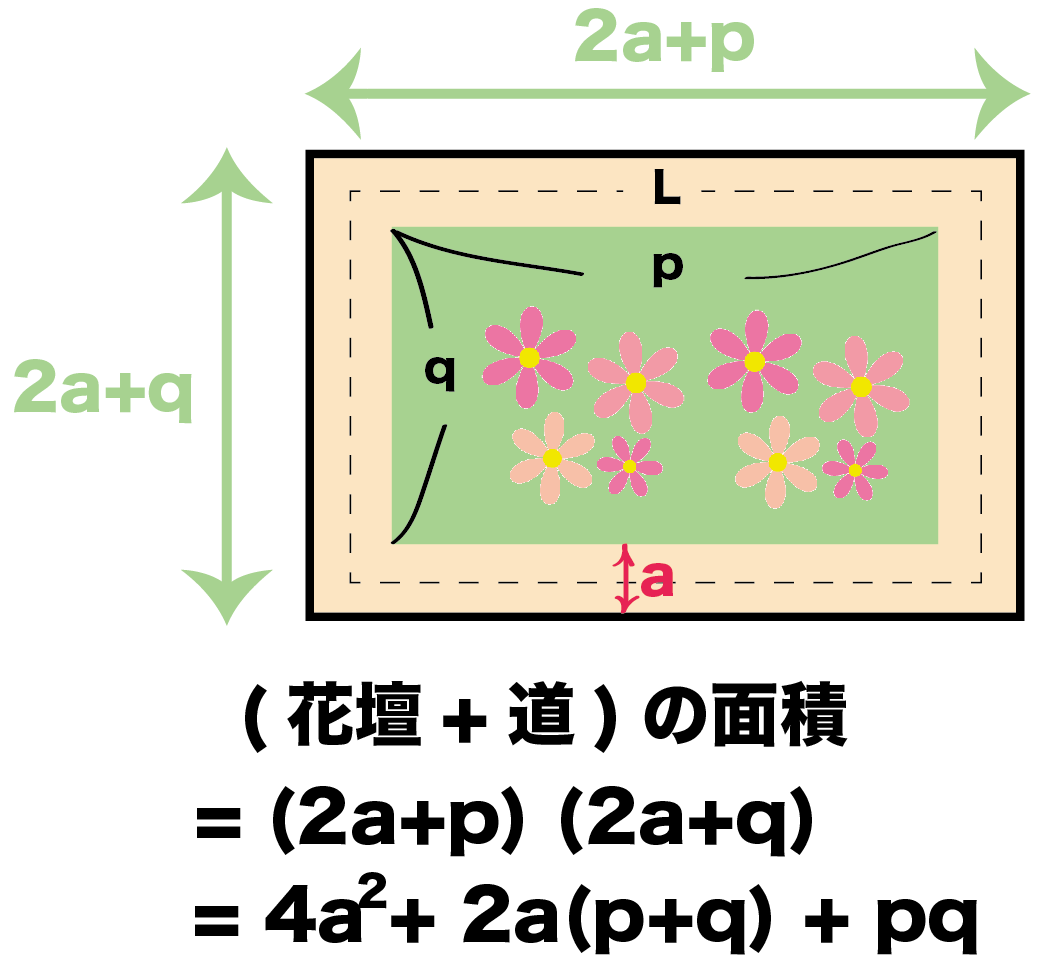



式の計算の利用 図形の証明問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿