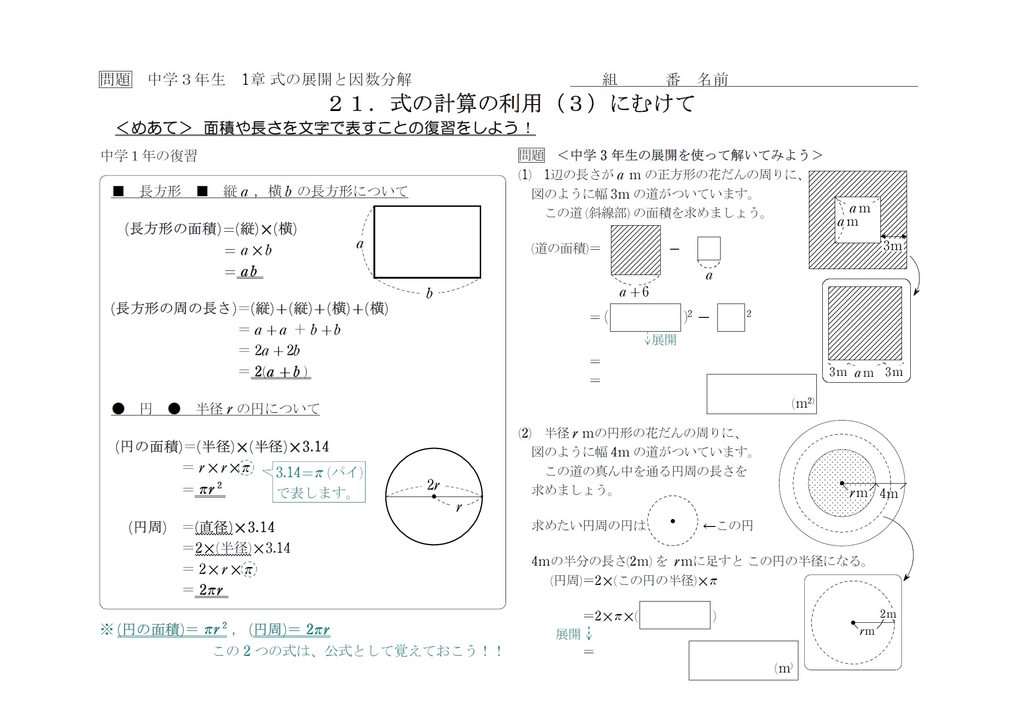
次の式を展開せよ。 (1) (2) ① 共通しているところを探しだして1つにまとめよう。 例 ② 中学で習った展開の式を思い出して、式を展開しよう。 ③展開後の式を整理しよう。 ・アルファベット順 例 a b c x y z ・降べきの順(次数の高いものから低いもの余因子展開とその応用 3 3 余因子展開の具体形 第i 行に関する展開は次のようになる。 fl fl fl fl fl fl fl fl fl fl fl fl fl fl fl fl fl fl fl fl fl a11 a12 a13 ¢¢¢ a1n a21 a22 a23 ¢¢¢ a2n ¢¢¢ ai1 ai2 ai3 ¢¢¢ ain ¢¢¢ an1 an2 an3 ¢¢¢ ann fl fl flこの展開の計算の中で、もっとも応用なのが次のような計算です。 $$\Large{2(a2)(a3)(a4)^2}$$ うげぇ かっこがたくさんあって複雑じゃ それでは、このような複雑な式の展開はどのように計算していけば良いのでしょうか。

高校数学 数 7 展開 3次式の公式編 Youtube
式の展開 応用
式の展開 応用-数学Ⅰ eテレ 毎週 月曜日 午後2:10~2:30 ※この番組は、21年度の新作です。高校講座home >> 数学Ⅰ >> 第4回 数と式 式の展開と因数分解の応用;




式の展開 やり方 公式 ツール 具体例で学ぶ数学
式の展開の工夫~置き換えを利用~ 問題の解説~置き換えのやり方~ 式の展開の工夫~組み合わせ、計算順序を考える~ 問題の解説~計算の順序~ 問題の解説~組み合わせ~ まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! 多項定理 (abc) n の展開式の係数; N を非負整数全体の集合とする。 Sn を {1,,n} から {1,,n} への全単射全体とする(n 次対称群)。 置換 σ∈Sn に対し sgn σ を σ の符号とする。 idn∈Sn を
基本的な乗法公式(展開公式) I (ab)2=a22abb2 II (a−b)2=a2−2abb2 III (ab) (a−b)=a2−b2 ※ これらの公式のうち I~ IVは中学校の復習となっているが,高校の数学 I でもう一度出てくる.公式は中学校と同じでも,扱い方が少し変るところがある数学Aで学んだ組み合わせの計算を多項式の展開に応用することが出来る。 () を展開することを考える。これは、 () () () () という式を展開したものであり、その係数は "n個の(ab)の中からいくつのa(またはb)を選ぶか"で決めることが出来る。 今回は難関レベルの展開の典型的なパターンを見ていこう。 なお、高校生以上の場合、今回紹介する問題は基礎問題なので、確実にできるようにした方がよい。 ←前回 展開の工夫と練習問題 (1) (標) →次回 因数分解の基本と練習問題 (基) 関連記事 11式
練習 次の式を展開せよ。 d e f \ <展開の応用Ⅱ> $ % $% を利用する展開。たとえば,教科書s 例題2で, d e d e d de e d de e と, つの をそれぞれ先に展開してしまうと,後の計算が面倒に なる。教科書の解答が要領のよい計算である。以上で、中学で学習する展開公式は完了になります^^ 次は、展開公式を利用した応用問題?というか計算ミスが起こりやすそうな問題を取り上げていきます。 分数が出てくる展開 展開の計算において、分数が含まれているモノは計算ミスが多発します。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru




中学数学 多項式 の教え方 展開の応用問題




式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく
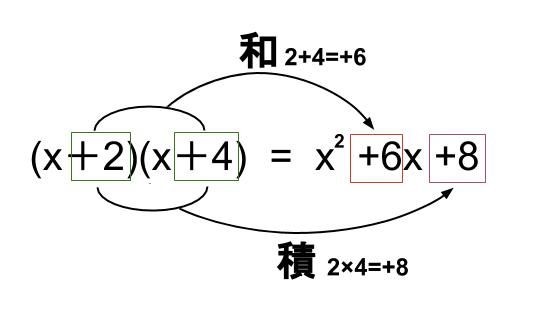
式の展開と因数分解の応用 5 5/10 実数、有理数、無理数 6 5/17 ルートの基本計算 7 5/24 有理化 8 5/31 無理数の近似値 9 6/7 1次不等式を先に公式を暗記するより、まずは分配法則をつかって確実に展開できるようになってから公式を覚えたほうが上達も早く、応用にもつよくなる。 (例) (x3)(x5) の展開 (x3)(x5) = x 2 5x 3x 15 = x 2 8x 15 5xと3xは同類項なのでまとめておく。 確認 展開せよ物理のための 応用数学 小出昭一郎・阿部龍蔵 監修/ 元 明治大学教授 理博 小野寺嘉孝 著 A5判/236頁/定価2970円(本体2700円+税10%)/19年3月発行 ISBN (旧ISBN ) C3042 理工系の学生が大学2年から専門課程で主として物理を学ぶ




高校入試合格bon 数学
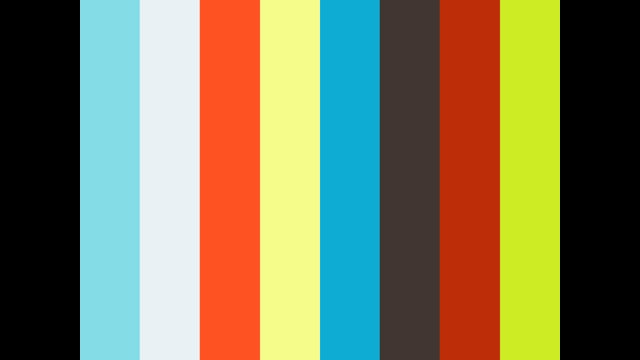



3 22第1章式の計算の利用 数の計算への応用 中学生
桃 == 置き換えによる展開 == 置き換えによる展開とは 同じ式が2回以上登場するとき,これらに名前を付けて1文字で表わす と,「見やすく」「間違いにくく」なる.ここでは2回以上登場する式を1文字で置き換えて展開の計算を行うことを考える. 例1 (a 高校の数学Ⅱで扱う文字式の展開の基本問題から応用問題までの練習です。 主に変形に利用するのは3次式の展開公式です。 展開は乗法公式を使わなくても必ずできますが、手順によっては処理が早くなる問題も少なくありません。 ある程多項式 例題 多項式と単項式の乗法除法 式の展開 乗法公式(xa)(xb)の展開 乗法公式 2乗の展開 乗法公式 和と差の積の展開 式の展開 いろいろな計算 式の展開 四則 因数分解1_共通因数をくくりだす 因数分解2_(xa)(xb) 因数分解3_2乗 因数分解4_(xa)(xa) 因数分解 おきかえ 共通因数をくくりだした後



Studydoctor乗法公式を利用する式の計算 中3数学 Studydoctor




1講 3次式の展開と因数分解 1節 式と計算 問題集 1章 式と証明
因数分解~基礎から応用まで 高校の数学では,最初に「数と式」という分野を学習します(数学 i )。 ここでは、単項式や多項式、それに整式、式の展開公式などを学びますが、その次に待ち受けているのが「因数分解」です。 因数分解は、数学 i だけでなく今後の数学でずっと登場す3 応用例1:誤差評価付きの近似値計算(ネイピア数e,無理数 √ 17) 4 応用例2:不定形の極限,増加速度の比較 5 応用例3:高校物理における近似式の精度 6 応用例4:円周率の計算 7 応用例5:漸近展開による不定形の極限計算 8 応用例6:漸近展開による関数本時の課題は、できるだけ生徒の身近な生活の中でイメージできるような内容にする。 ③ 本時の課題やその提示に当たっては、生徒の興味・関心を喚起するような工夫をする。 ④ 本時の課題をつかませる際は、具体物やプレゼンテーションソフトを




展開 6 ストレートクロスの応用 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学 数 6 展開 応用編 Youtube
常微分方程式の解の漸近展開とその応用 お茶の水女子大学 渋 谷 泰 隆 解の性質を詳しく調らべなければならないとぎ には,そ のために都合のいい形をした近似を作る ことが必要になる近 似の作り方にも色々あるが 漸近展開もその一つであるこ の報告こちらを二項定理を使って展開をしていくと、 一般項は次のような形になり、 になるための の値を見つけることができます。 になることが分かれば、一般項にあてはめて計算をしていきましょう。 よって、 の係数は であることが求まりました。 答え3項の式の展開 例題1 次の式を展開しなさい。 \((xy1)^2\) 解説 まともに計算すると \(9\) 回かけ算です。 \(xy\) を \(1\) かたまりとして扱うのがおススメです。 \(\{(xy)




二項定理の公式と証明をわかりやすく解説




基礎編 数学の 式の展開 でつまずいたらココを見直そう まなビタミン
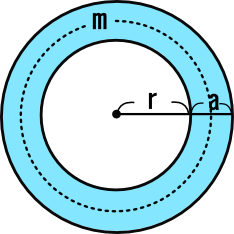
== 展開公式の応用問題 == (1回目の因数分解をした後の式で、2つめの()で括られている部分の符号が違う) 私の指摘が間違っているようでしたら、なぜそれが間違いなのかの解説もいただけると助かります。 =>作者:連絡数学31章式の展開と因数分解「多項式の乗法」<応用問題②・解答> 4つの数の組の,左上の数に注目する。 かけられる数(たての数)をm,かける数(横の数)をn とすると,左上の数はmnと表せる。 mn m(n+1) 左下の数は(m+1)n※この番組は、21年度の新作です。 10 6/14 1次方程式・1次不等式の応用 11 6/21 2次関数 関数 12 6/28 2 次関数の頂点 13 7/5 2 次関数のグラフをかく 14 7




式の展開 やり方 公式 ツール 具体例で学ぶ数学




高校数学 数 7 展開 3次式の公式編 Youtube
ツイート 中学3年生の数学 練習問題プリントです。 家庭学習用の練習プリントとして、またテスト前の確認などにもご利用ください。 式の展開と因数分解 平方根 2次方程式 2次関数 図形の相似 三




高校数学 展開の工夫 共通部分の置き換え 受験の月




中3数学 式の展開の公式 やり方についてわかりやすく説明しました 都立高校受験応援ブログ




中3 中3数学 式の計算の利用 中学生 数学のノート Clear




中3数学 道路の面積を求める問題 例題編 映像授業のtry It トライイット
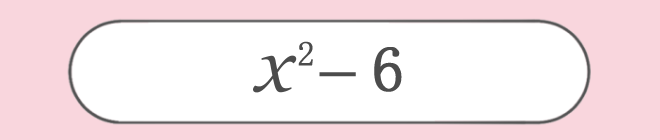



数学 時短演習cote



数と式の問題 Of 京極一樹の数学塾会員頁




数学 中3 11 式の計算の利用 くふう編 Youtube



1



中学3年数学練習問題 式の利用 証明 式の展開 因数分解の応用




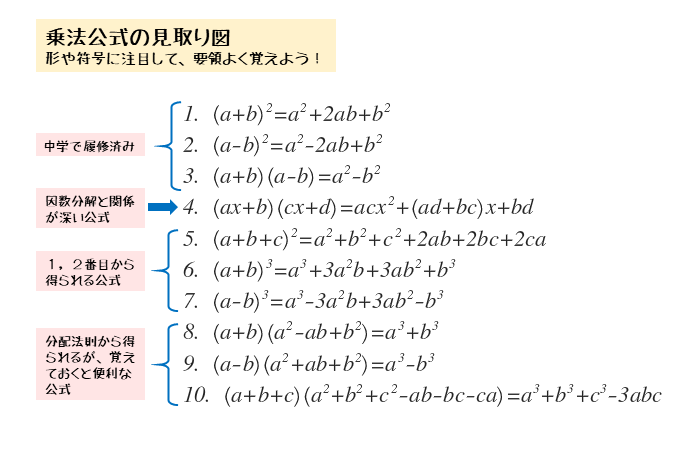
乗法公式 式の展開公式 19個まとめ 高校数学の美しい物語




展開 6 ストレートクロスの応用 怜悧玲瓏 高校数学を天空から俯瞰する
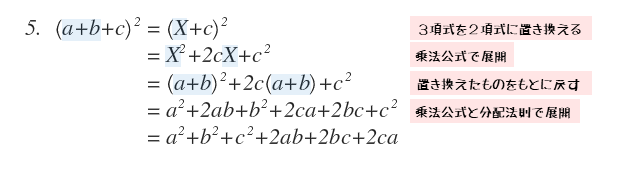



数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん




中3数学 複雑な式の展開をマスターしよう 数スタ



中学校3年生式の展開 因数分解分野応用問題 中学3年生の数学の授業で Yahoo 知恵袋




無料 中3数学 発展 応用問題 問題プリント 305 式の計算5 因数分解1



1




公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局




中学数学 多項式 の教え方 展開の応用問題



数と式 整式の展開に関する問題を解いてみよう 日々是鍛錬 ひびこれたんれん




中3 式の計算 因数分解 公式編 設計図の選び方と使い方 あとはパズル 教えたい 人のための 数学講座




高校数学 展開公式の利用 受験の月



2
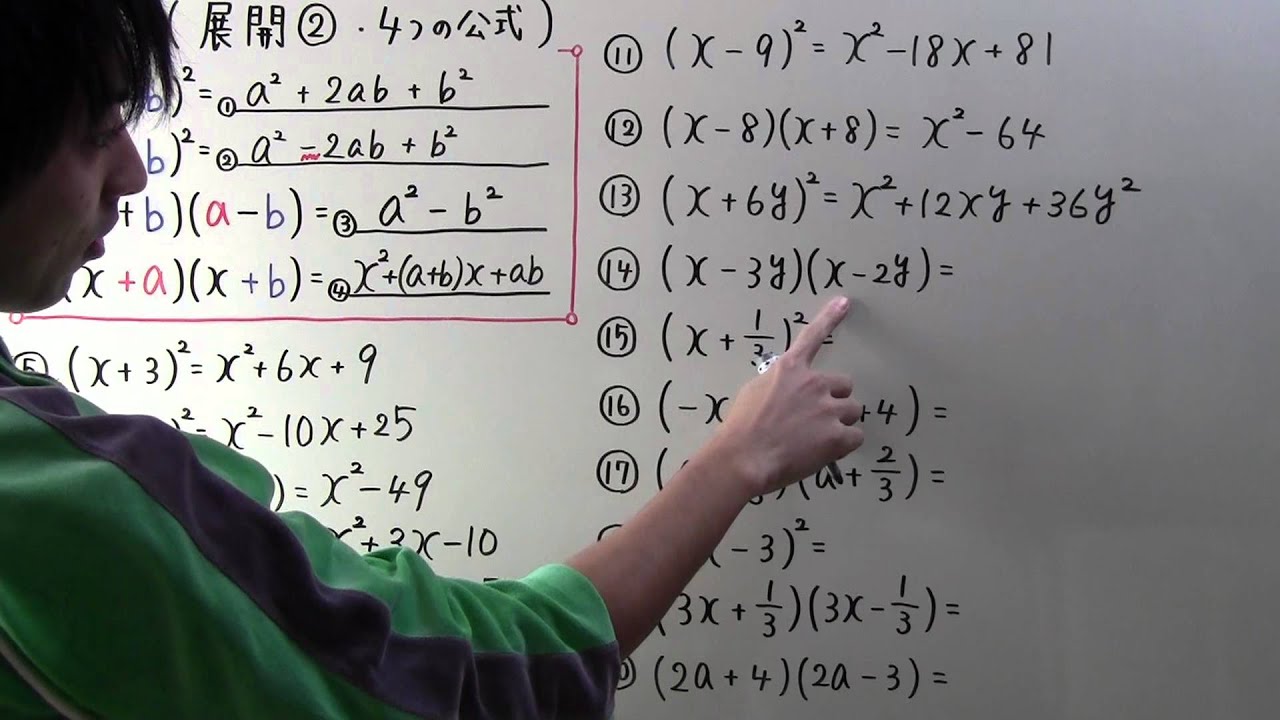



数学 中3 3 展開 4つの公式 Youtube



Studydoctor3項式の展開 中3数学 Studydoctor




中3数学 式の展開 因数分解がスラスラ解ける 魔法の授業 学校 塾 家庭教師の1カ月分が1本の動画に On Vimeo



3




基礎編 数学の 式の展開 でつまずいたらココを見直そう まなビタミン




式の計算の利用と練習問題 基 数学の解説と練習問題




中3数学 複雑な式の展開をマスターしよう 数スタ
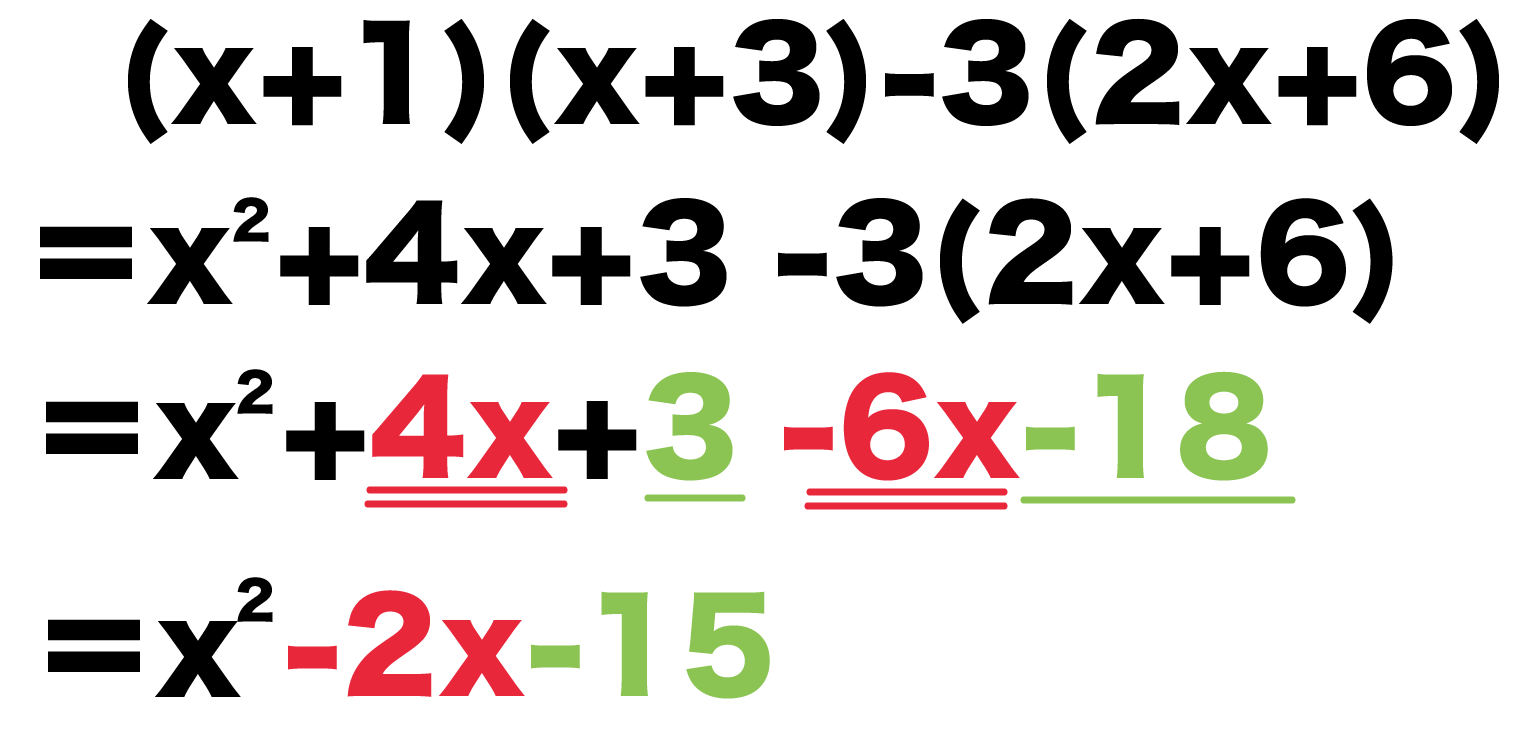



中学数学 式の展開の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
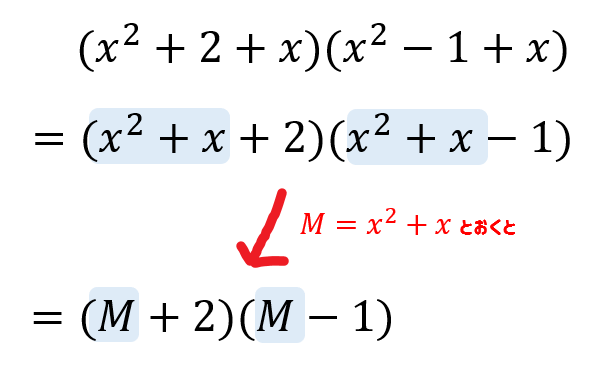



高校数学 式の展開の工夫 置き換えや組み合わせを利用するやり方を解説 数スタ



乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係




数学 A B C 二乗の展開公式は 問題の解き方は徹底解説 数スタ




中3 中3数学 式の計算の利用 中学生 数学のノート Clear




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




式の計算の利用と練習問題 基 数学の解説と練習問題




Studydoctor3項式の展開 中3数学 Studydoctor




展開因数分解の式の値の応用 対称式と交代式 中3数学 高校受験ラボ



中3自習 展開と因数分解 1 中学数学の勉強に




数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん




中3数学 式の展開とはなにものか Qikeru 学びを楽しくわかりやすく




高校数学 式の展開の工夫 Youtube



1




メルカリ 受験生のための基礎計算問題集 計算タイムトライアル中3 本 1 500 中古や未使用のフリマ
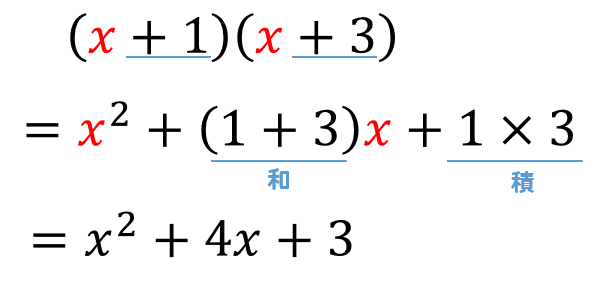



中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ
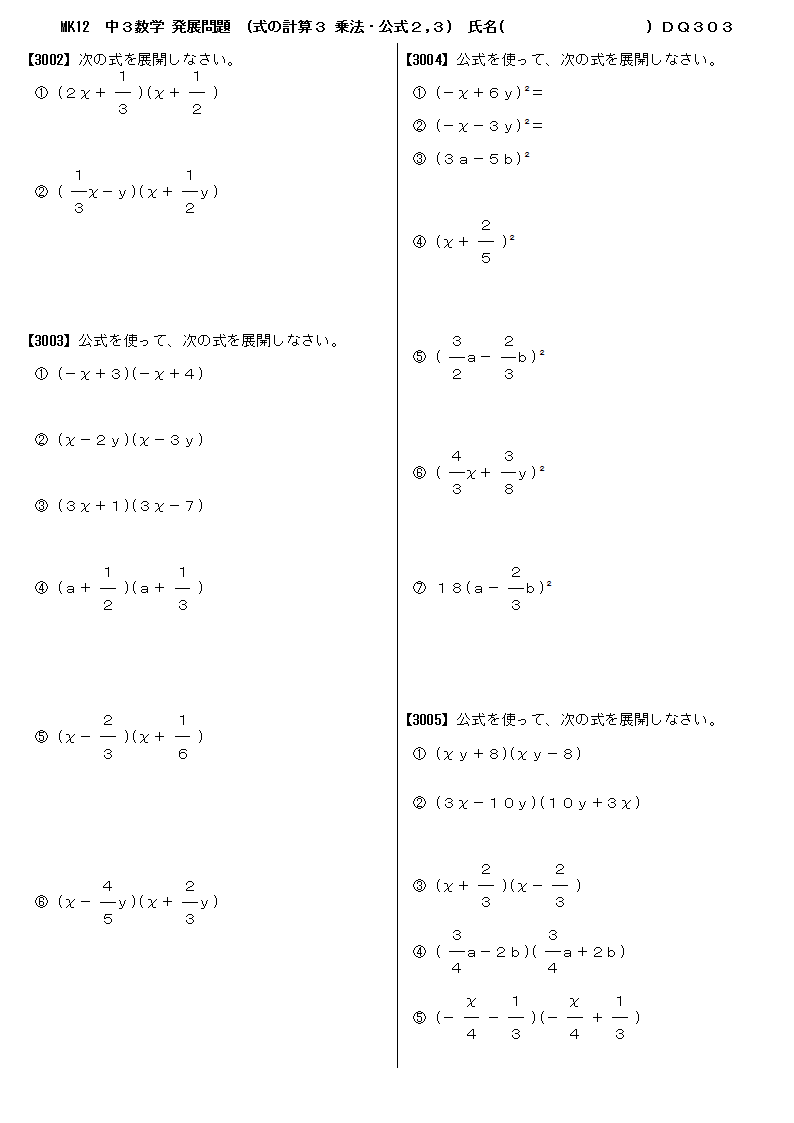



無料 中3数学 発展 応用問題 問題プリント 303 式の計算3 乗法 公式2 3




数学 時短演習cote




基本 三次式の展開 なかけんの数学ノート




高校数学 二項定理 A B Nの展開式 整式の係数の和 受験の月



中3数学 式の展開 応用まで 横井学院予備校のブログ




勉強しよう数学解答集 因数分解の応用問題の問1の解答



展開と因数分解 中学3年の数学 数学の旋律




高校数学 サクシード 全問解説 数学 カリスマ塾長 タイガーblog
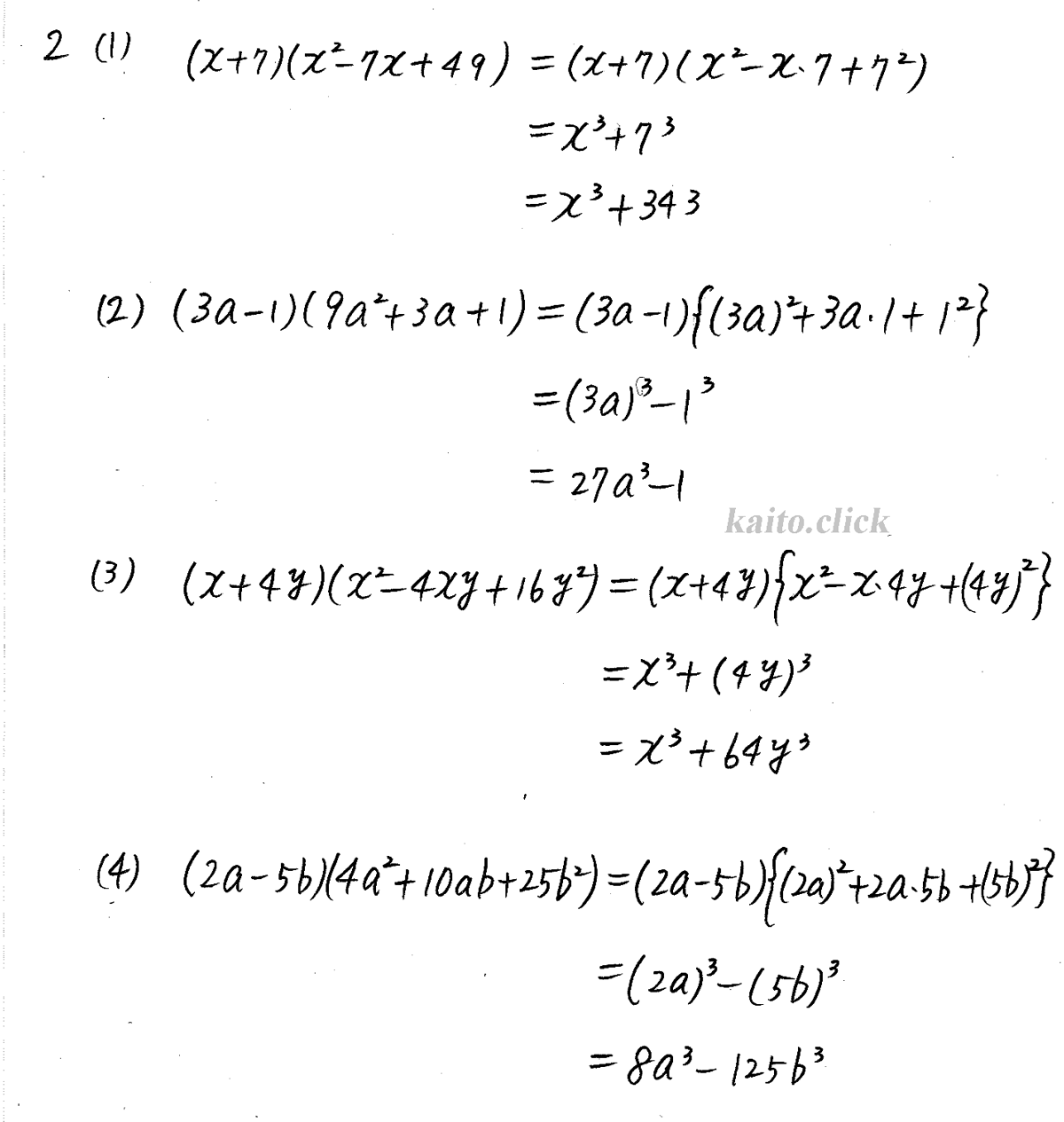



クリアー数学 数2 P6 1 3次式の展開と因数分解




中学3年生 数学 式の活用 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
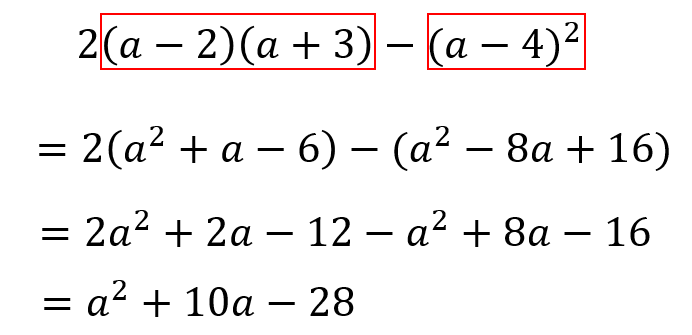



中3数学 複雑な式の展開をマスターしよう 数スタ




式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく




高校数学 多項定理 A B C Nの展開式の係数 受験の月



展開公式




中3 数学 式の展開と因数分解 東京都稲城市の個別塾 学習塾 ナビ個別指導学院 稲城校ブログ




式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく
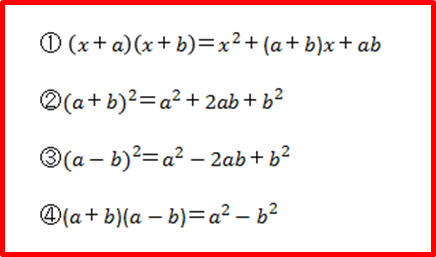



中3数学 式の展開 浦添ベスト進学教室




中学3年数学練習問題 式の利用 証明 式の展開 因数分解の応用




乗法公式 無料で使える中学学習プリント




中学数学 式の展開 因数分解




交代式の因数分解と実践的な例題 高校数学の美しい物語




式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく



中学数学 式の展開 乗法公式 中学数学の無料オンライン学習サイトchu Su




中3数学 式の展開とはなにものか Qikeru 学びを楽しくわかりやすく
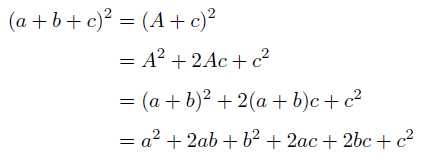



置き換えによる式の展開 まなびの学園



因数分解とは 公式や計算のやり方 問題の解き方 受験辞典



展開公式



数と式の問題 京極一樹の数学塾




動画授業コース 中3数学 式の展開 因数分解 ます 学校 塾 家庭教師の1カ月分が1本の動画に 勉強 受験 学習方法の相談 ココナラ




三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ




中3数学 展開とは 練習編 映像授業のtry It トライイット




中学数学 多項式 の教え方 展開の応用問題
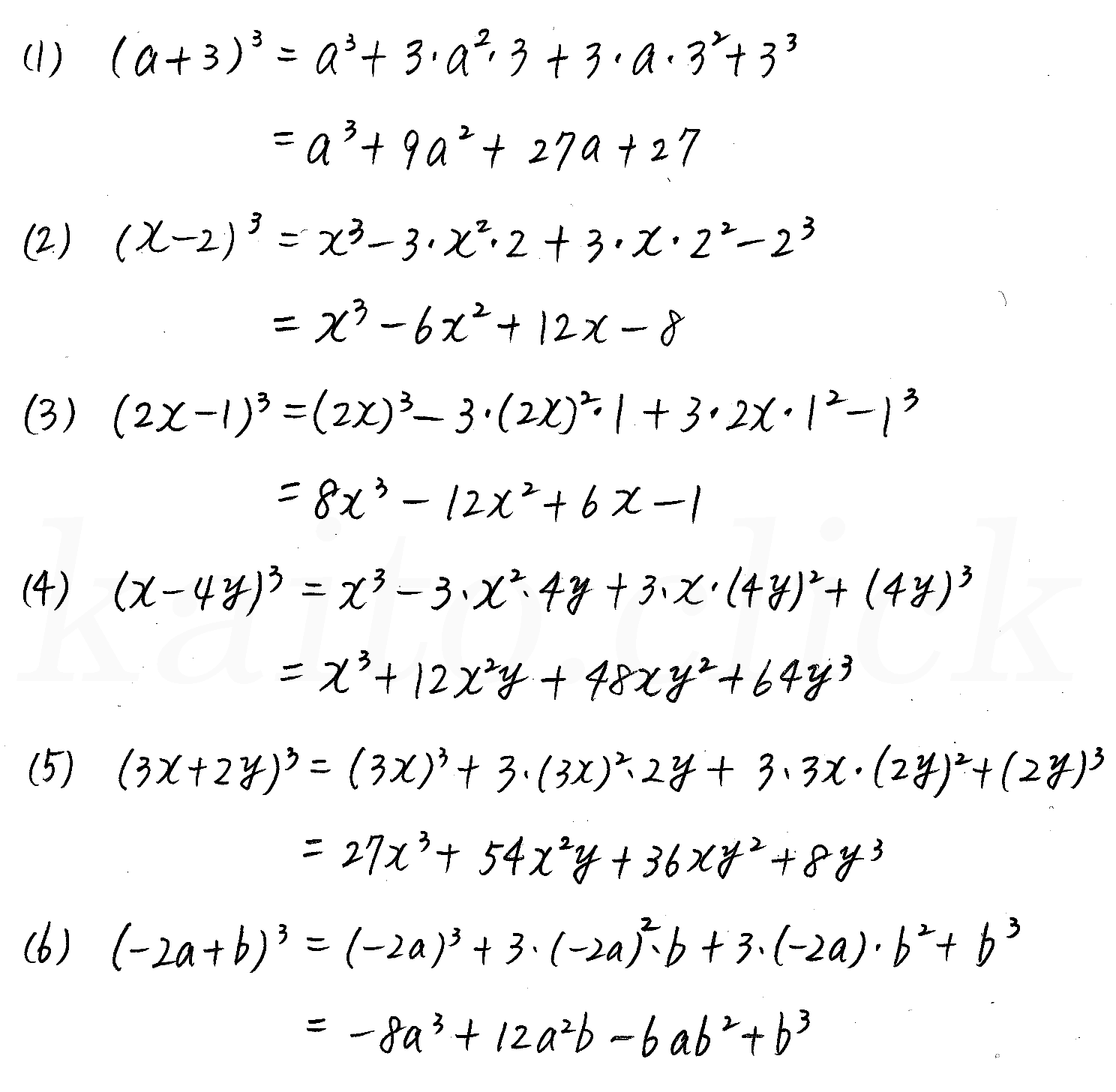



改訂版 3trial数学 P6 1 3次式の展開と因数分解




二項定理とは 公式と係数の求め方 応用までをわかりやすく解説




中3 式の計算 因数分解 応用編 基本の理解で組立ok 難問と勉強の取組みについて 教えたい 人のための 数学講座




中学3年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




3次式 4次式の因数分解と高次方程式の解法 数学の偏差値を上げて合格を目指す
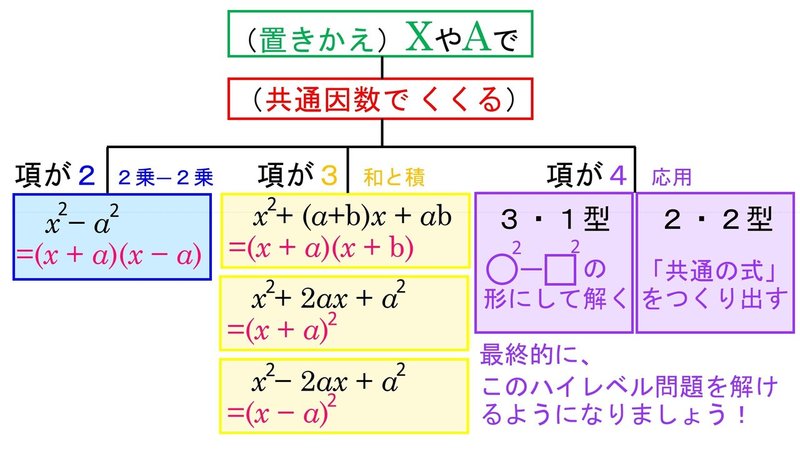



中学3年 数学 式の展開 因数分解 学校の先生 塾 家庭教師講師用 オンライン授業用パワーポイントスライド 教材制作が楽に 指導者用 オンライン家庭教師 オンライン授業マジック先生 小学生 中学生 5教科受け放題 Note




去年の今日日記 中3式の展開応用編ドーナツ型の道の面積証明 都立入試の情報満載 こじんまりしたこじま塾ブログ




展開の公式 三次式の展開 Youtube




ヤフオク 因数分解の中古品 新品 未使用品一覧




中学数学 多項式 の教え方 展開の応用問題
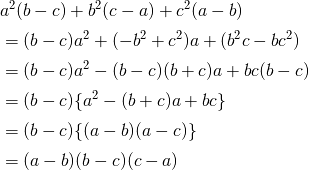



公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局




中3 展開と因数分解8 動画 いろいろな展開 レベル3の解説 中学数学の勉強に




式の展開 無料で使える中学学習プリント




中3 中3数学 式の計算の利用 中学生 数学のノート Clear




三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ



0 件のコメント:
コメントを投稿